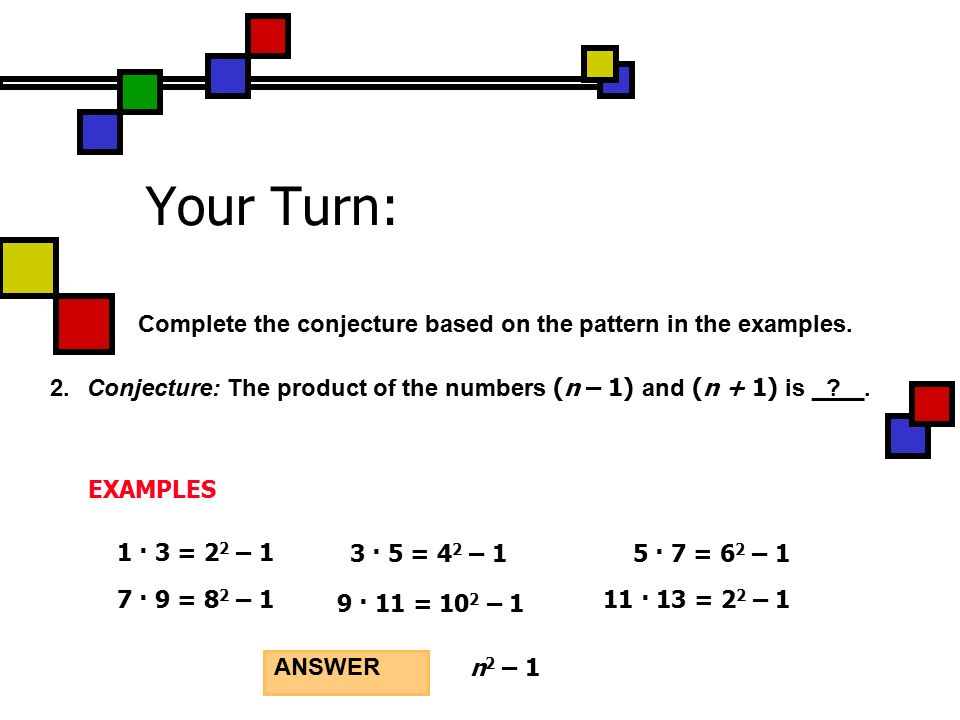
Conjecture 2 3 5 7 11

Twin prime conjecture also known as polignac s conjecture in number theory assertion that there are infinitely many twin primes or pairs of primes that differ by 2. By convention 1 is a not considered to be a prime number. A prime number is a positive integer which has exactly 2 positive integer factore one factor being 1 and the other factor is the positive number itself.

concert anul nou viena 2018 concediul de odihna codul muncii 2017 concert europa fm live pe plaja 2018 concediu fara plata invatamant preuniversitar concert din muzica de bach film concert ed sheeran 3 iulie concediu medical ingrijire copil medic familie concert andrea bocelli 2017 cluj

What Is The Next Number In The Series 2 3 5 7 11 13 17 Quora

Solved A Prime Is An Integer That Can Only Divisible By 1 Chegg Com

Solved A Prime Is An Integer That Can Only Divisible By I Chegg Com

2 2 Patterns Inductive Reasoning Ppt Download

Gilbreath S Conjecture From Wolfram Mathworld

Inductive Reasoning Section 1 2 Objectives Use Inductive Reasoning To Make Conjectures Ppt Download

2 3 5 7 11 13 17 19 23 29 31 37 show that goldbach s conjecture is true for the even numbers from 20 to 40 by writing each number as a sum of two primes.

Conjecture 2 3 5 7 11. Gilbreath was doodling on a napkin. The sequence of gaps the differences between each prime and the next is 1 2 2 4 2 4 2 4 6 2 6 4 2 and 4. 6 3 3. The primes up to 50 are 2 3 5 7 11 13 17 19 23 29 31 37 41 43 and 47.

2 3 5 7 11 13 conjecture. 2 3 5 7 11 13 17 19 23 29. 42 is the next number in this sequence. 2 3 5 7 11 13 17 3 2 1 5 3 2 7 5 2 11 7 4 13 11 2 17 13 4 therefore the next number is obtained thus.

X 17 2 x 19 ans. 4 2 2. The rest of the gaps are even numbers. 8 3 5.

In 1958 norman o. However the sequence 2 3 5 7 11 are the first five prime numbers. I ve illustrated the goldbach conjecture for some even numbers below. Answer by jim thompson5910 35256 show source.

2 2 1 3 3 2 5 5 2 7 7 4 11 11 2 13 13 4 17 next term 17. This number sequence is adding the next prime number to the last number. He started by writing down the first few primes. 100 3 97 or 11 89 or 17 83 or 29 71 or 41 59 or 47 53.

So 1 2 3. As numbers get larger primes become less frequent and twin primes rarer still. The number 1 appears only once because all primes except for 2 are odd. 10 5 5 or 3 7.

Find an answer to your question 4. For example 3 and 5 5 and 7 11 and 13 and 17 and 19 are twin primes. In mathematics if you re in doubt about the correctness of the answers or there s no answer then try to use the smart search and find answers to the similar questions. Then 3 3 6 6 5 11 11 7 18 18 11 29.

2 3 5 7 11 13 17 19 etc. So the next prime numbers after 11 are 13 then 17 19 23 29 31 37 41 43. Clearly all prime numbers other than 2 must be odd.